
BOJ No.1626 [두 번째로 작은 스패닝 트리]
문제
1626번: 두 번째로 작은 스패닝 트리 (acmicpc.net)
1626번: 두 번째로 작은 스패닝 트리
첫째 줄에 그래프의 정점의 수 V(1 ≤ V ≤ 50,000)와 간선의 수 E(1 ≤ E ≤ 200,000)가 들어온다. 둘째 줄부터 E+1번째 줄까지 한 간선으로 연결된 두 정점과 그 간선의 가중치가 주어진다. 가중치는 100,
www.acmicpc.net
설명
<알고리즘 분류>
* 최소 스패닝 트리 / 최소 신장 트리 (MST)
* 최소 공통 조상 (LCA)
먼저 최소 스패닝 트리(MST) 를 먼저 구해야 한다. 두 번째로 작은 스패닝 트리는 앞서 구한 MST 보다 총 가중치의 값은 최소한으로 늘어나야 한다.

문제에서 예제 입력을 가지고 최소 스패닝 트리와 두 번째로 작은 스패닝 트리를 구현 해 보았다. 최소 스패닝 트리에서 하나의 간선이 다른 간선으로 바뀐 것을 확인할 수 있다. 또한 총 가중치의 합이 42 에서 44로 늘어났다.
만약, {4}---{7} 간선의 가중치가 12 였다면 위와 같이 두 번째로 작은 스패닝 트리가 정의되지 않았을 것 이다. 이는 결국 트리의 형태만 다를뿐 총 가중치의 합은 최소 스패닝 트리와 같게 될 것 이므로, 최소 스패닝 트리의 다른 형태에 불과하기 때문이다.
요점은 MST 에서 하나의 간선을 사용되지 않은 간선 중 하나로 바꾸는 것 이다. 이 때 MST 에서 없앨 간선을 중심으로 확인하지 않고 사용되지 않은 간선들 하나하나를 중심으로 확인을 하게 된다. 사용되지 않은 간선들 중 하나를 선택하여 MST 에 추가를 하면 무조건 사이클이 한 개 발생하게 된다. 즉, 간선을 추가함으로서 생긴 사이클에 해당되는 간선들 중 하나를 제거해야 한다.
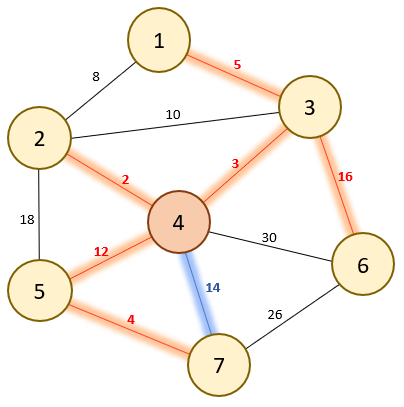
사이클을 파악하기 위해선 최소 공통 조상(LCA) 알고리즘을 사용하였다. 위 사진은 기존 MST 그래프에서 {4}---{7} 간선을 추가 해 보려고 하는 상황이다. 이 경우에는 4번 노드와 7번 노드의 사이클을 파악하기 위해 이 두 노드의 LCA 를 파악해야 한다.

사이클을 파악하기 위해 LCA 를 파악하는 이유는 이렇게 설명할 수 있다. {a} 노드와 {b} 노드를 예시로 들 때 위 {e} 노드를 루트노드로 가지는 MST 그래프 (빨간색 그래프) 에서 {a} 노드와 {b} 노드의 LCA는 {d} 이다. LCA는 결국, {a}, {b} 노드가 계속해서 그래프를 타고 올라가다가 처음으로 만나는 지점이며 그래서 {a}---{b} 간선을 추가 함으로써 사이클이 발생되는 지점인 것 이다.
사이클을 파악 한 뒤에는 사이클에 해당되는 간선들 중 어떠한 간선을 없애야 총 가중치의 값이 MST 에서 가장 조금만 늘어날 수 있는지 확인을 하면 된다. 가장 조금만 늘어나는 경우를 파악하는 이유는, 두 번째로 작은 스패닝 트리를 구해야 하기 때문이다. 가장 조금만 늘어나는 경우를 파악하지 않는다면 완성된 트리가 몇 번째로 작은 스패닝 트리인지는 모를 것 이다.
따라서 모든 사용되지 않은 간선들에 대해서 LCA 를 찾고 사이클을 파악하여 그 사이클 내부 간선들 중 가장 적합한 간선들을 없애보면서, 새로운 트리의 가중치의 값을 계산하고 계산된 가중치의 값들 중 가장 최소값을 가지는 트리가 "두 번째로 작은 스패닝 트리" 가 될 것 이다. 이 때 조심해야 할 점은 아까 말했듯 추가되는 간선과 같은 가중치의 값을 가지는 간선을 없애면 안된다. 이 경우는 그냥 다른 형태의 MST가 되는것에 불과하기 때문이다.
<정리>
1. MST 를 파악한다.
2. MST 를 파악하면서, 사용되지 않는 간선들을 정리한다.
3. 사용되지 않는 간선들을 하나하나 확인 할 것 이다.
4. 대체하려는 간선(사용되지 않은 간선)을 MST 트리에 추가함으로써 생기는 사이클에서 대체되기 가장 적합한 간선을 없앤다.
(사이클은 LCA 를 통해 확인한다.)
5. 이렇게 사용되지 않은 간선들에 대해서 모든 케이스를 확인해 본 후 가장 최소의 가중치 합 값을 가지는 경우가 두 번째로 작은 스패닝 트리의 가중치의 합이 된다.
Code
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
using namespace std;
struct Node {
int a, b;
int dist;
};
struct LCA_Node {
int node;
int dist;
};
struct comp {
bool operator ()(Node A, Node B) {
if (A.dist < B.dist) return false;
else if (A.dist > B.dist) return true;
else if (A.a > B.a) return true;
else return false;
}
};
priority_queue<Node, vector<Node>, comp> pq;
priority_queue<Node, vector<Node>, comp> notUsed;
vector<vector<LCA_Node>> adj;
vector<LCA_Node> parentLCA;
vector<int> depth;
vector<int> parent;
const int inf = 1e9;
int V, E;
void DFS(int curNode, int dpth) {
int size = adj[curNode].size();
depth[curNode] = dpth;
for (int i = 0; i < size; i++) {
if (depth[adj[curNode][i].node] == -1) {
parentLCA[adj[curNode][i].node] = { curNode, adj[curNode][i].dist };
DFS(adj[curNode][i].node, dpth + 1);
}
}
}
int LCA(int a, int b, int tarDist) {
int smallestUpgrade = inf;
// depth 를 맞춘다
if (depth[a] < depth[b]) {
int diff = depth[a] - depth[b];
int curDist;
while (depth[a] != depth[b]) {
curDist = parentLCA[b].dist;
b = parentLCA[b].node; // b update
if (tarDist == curDist) continue;
smallestUpgrade = min(smallestUpgrade, tarDist - curDist);
}
}
else if (depth[a] > depth[b]) {
int diff = depth[b] - depth[a];
int curDist;
while (depth[a] != depth[b]) {
curDist = parentLCA[a].dist;
a = parentLCA[a].node; // a update
if (tarDist == curDist) continue;
smallestUpgrade = min(smallestUpgrade, tarDist - curDist);
}
}
// 조상 노드를 확인한다
int aTemp = a, bTemp = b;
int curDist;
while (aTemp != bTemp) {
curDist = parentLCA[aTemp].dist;
if (curDist != tarDist)
smallestUpgrade = min(smallestUpgrade, tarDist - curDist);
curDist = parentLCA[bTemp].dist;
if (curDist != tarDist)
smallestUpgrade = min(smallestUpgrade, tarDist - curDist);
aTemp = parentLCA[aTemp].node;
bTemp = parentLCA[bTemp].node;
}
return smallestUpgrade;
}
int Find(int a) {
if (parent[a] == a) return a;
else return parent[a] = Find(parent[a]);
}
void Union(int a, int b) {
int pa = Find(a);
int pb = Find(b);
parent[pb] = parent[pa];
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> V >> E;
parent.assign(V + 1, 0);
adj.resize(V + 1);
depth.assign(V + 1, -1);
parentLCA.assign(V + 1, { 0, 0 });
for (int i = 1; i <= V; i++) parent[i] = i;
int a, b, dist;
for (int i = 0; i < E; i++) {
cin >> a >> b >> dist;
pq.push({ a, b, dist });
}
Node cur;
int ret = 0;
while (!pq.empty()) {
cur = pq.top();
pq.pop();
if (Find(cur.a) != Find(cur.b)) {
ret += cur.dist;
Union(cur.a, cur.b);
adj[cur.a].push_back({ cur.b, cur.dist }); // for LCA
adj[cur.b].push_back({ cur.a, cur.dist }); // for LCA
}
else notUsed.push(cur);
}
int tarUnion = 0;
for (int i = 1; i <= V; i++) {
if (1 < i) {
if (Find(i) != tarUnion) {
cout << "-1\n"; // MST 도 없는 case
return 0;
}
}
else tarUnion = Find(i);
}
DFS(tarUnion, 0); // tarUnion == rootNode
Node cur2;
int ret2 = inf;
while (!notUsed.empty()) {
cur2 = notUsed.top();
notUsed.pop();
ret2 = min(LCA(cur2.a, cur2.b, cur2.dist), ret2);
}
if (ret2 != inf)
cout << ret + ret2;
else cout << -1;
}'Algorithm (C++ based) > BOJ' 카테고리의 다른 글
| 백준 No.11266 [단절점] (0) | 2021.08.21 |
|---|---|
| 백준 No.1261 [알고스팟] (0) | 2021.08.17 |
| 백준 NO.13537 [수열과 쿼리 1] (0) | 2021.08.14 |
| 백준 No.14427 [수열과 쿼리 15] (0) | 2021.08.13 |
| 백준 No.8980 [택배] (0) | 2021.08.12 |




댓글