
BOJ No.7420 [맹독 방벽]
문제
7420번: 맹독 방벽
첫 번째 줄에 건물의 수 N과 거리 L이 주어진다. (3 ≤ N ≤ 1000, 1 ≤ L ≤ 1000, N과 L은 정수) 다음 N개의 줄에 거쳐 건물의 좌표 Xi와 Yi가 정수로 주어진다. (-10000 ≤ Xi, Yi ≤ 10000) 모든 건물의 좌
www.acmicpc.net
설명
<알고리즘 분류>
* 볼록 껍질 (컨벡스 헐 : Convex hull)
볼록 껍질을 응용하여 풀 수 있는 문제이다. 아래 예시를 들어 보았다.

건물들의 좌표를 위와 같이 입력을 해 보았다. 또한 해당 좌표들을 좌표평면에 표시 해 보았다. 위 좌표들을 모두 감싸면서 건물들에선 최소 L 만큼 떨어져 있어야 하는 방벽을 세워야 한다. 위 상황에서 L 값을 10 이라고 가정 해 보고 건물에서 L 만큼 떨어진 영역들을 표시 해 보았다.

위 상황을 보고 최소 길이의 방벽을 세운다고 할 때, 두 경우를 생각해 볼 수 있다.

두 경우 모두 모든 건물들을 최소 L 의 거리를 가진 방벽을 세운 상황들이다. 하지만, 방벽을 최소의 거리로 세워야 하므로, Case 2의 방법을 택해야 하는 것을 알 수 있다.
이 때 볼록 껍질(컨벡스 헐 : Convex hull) 알고리즘이 적용된다.
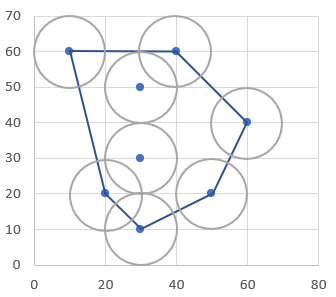
건물들에 대해서 컨벡스 헐 알고리즘을 적용한 상황은 위와 같다. 위 다각형을 활용하여 아래와 같은 경우까지 생각할 수 있다.

방벽의 길이를 생각할 때 곡선에 해당되는 부분은 위와 같이 L 길이의 반지름을 가지는 원의 둘레라는 것을 알 수 있으며, 직선(선분)에 해당되는 부분은 컨벡스 헐 알고리즘을 통해 만들어진 볼록 다각형의 둘레라는 것을 알 수 있다. 방벽의 총 길이는 이 두 값을 더한 것 이다. 아래 식과 같이 정리할 수 있다.

볼록 다각형을 이루는 좌표들은 Stack에 들어가게 된다. 이를 이용하여 한 좌표식 pop 을 하면서 Stack의 가장 위에 있는 두 좌표의 유클리드 거리를 계속해서 더해주면 방벽의 직선 길이를 알 수 있다.
<정리>
1. 컨벡스 헐 알고리즘을 통해 Stack 에 다각형을 형성하는 좌표들을 담는다.
2. 이 Stack을 통해 다각형의 둘레의 길이를 파악한다.
3. L 값을 통해 방벽의 곡선 에 해당되는 부분들의 길이를 파악한다.
4. 이 직선/곡선 길이를 더하여 방벽의 총 길이를 구한다.
Code
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <stack>
#define INF 999999999
#define RIGHT -1
#define LINE 0
#define LEFT 1
#define PI 3.1415926535
using namespace std;
typedef double MyType;
struct point {
MyType x, y;
};
int N;
MyType L;
point sp;
vector<point> arr;
stack<point> s;
MyType CCW(point A, point B, point C) {
MyType temp = (A.x * B.y) + (B.x * C.y) + (C.x * A.y);
temp -= (A.x * C.y) + (B.x * A.y) + (C.x * B.y);
if (temp > 0) return LEFT;
else if (!temp) return LINE;
else return RIGHT;
}
bool comp1(const point& A, const point& B) { // ORDER BY y ASC, x ASC
if (A.y != B.y) return A.y < B.y;
else return A.x < B.x;
}
bool comp2(const point& A, const point& B) { // 반시계방향으로 정렬
MyType dir = CCW(sp, A, B);
if (dir) return dir == LEFT;
else return comp1(A, B);
}
int main() {
cin >> N >> L;
MyType input_x, input_y;
for (int i = 0; i < N; i++) {
cin >> input_x >> input_y;
arr.push_back({ input_x, input_y });
}
sort(arr.begin(), arr.end(), comp1); // 점들을 y, x 값을 기준으로 오름차순 정렬한다.
sp = arr[0]; // sp 에 시작점 좌표를 대입한다.
sort(arr.begin() + 1, arr.end(), comp2); // 점들을 시작점 기준으로 반시계방향으로 정렬한다.
// Convex huE 본격적으로 시작!
point p1, p2, p3;
p1 = sp; s.push(p1); // Stack에 시작점을 넣는다.
p2 = arr[1]; s.push(p2); // Stack에 시작점 바로 다음 점을 넣는다.
for (int i = 2; i < N; i++) {
p3 = arr[i]; // 현재 점
while (1 < s.size()) {
p2 = s.top(); s.pop(); // first, second, third 를
p1 = s.top(); // 정의하기 위해 Stack에서 잠시 뺀다.
if (CCW(p1, p2, p3) == LEFT) { // p1, p2, p3 점 세 개로
s.push(p2); // 볼록 다각형과 같이 점이 잘 연결 되었다면
break; // Stack에 아까 뺀 두 번째 점을 다시 넣는다.
}
}
s.push(p3); // third 점을 Stack에 넣는다.
}
s.push(sp);
MyType ans = 2.0 * L * PI; // 방벽의 곡선 길이로 초기화를 한다.
point P1, P2;
while (!s.empty()) {
P1 = s.top(); s.pop(); // 이와 같이 다각형의 둘레를 구하기 위한
if (s.empty()) break; // 두 좌표값을 얻는다.
P2 = s.top(); // Stack에 아무 좌표도 들어있지 않으면 종료한다.
MyType X = abs(P1.x - P2.x); // 두 좌표의 가로 길이
MyType Y = abs(P1.y - P2.y); // 두 좌표의 세로 길이
ans += sqrt(X * X + Y * Y); // P1, P2 좌표로 이루어진 직선 길이를 더한다.
}
cout << round(ans);
}참고하면 좋은 개념들
2022.03.27 - [Algorithm (C++ based)] - 볼록 껍질 (컨벡스 헐 : Convex hull)
볼록 껍질 (컨벡스 헐 : Convex hull)
볼록 껍질 (컨벡스 헐 : Convex hull) 점들을 통해 볼록 다각형을 형성 다각형에 포함되지 않는 점들은 다각형 내부에 존재 참고 링크 2022.03.26 - [Algorithm (C++ based)/BOJ] - 백준 No.1708 [볼록 껍질] 백준..
johoonday.tistory.com
'Algorithm (C++ based) > BOJ' 카테고리의 다른 글
| 백준 No.1019 [책 페이지] (0) | 2022.04.13 |
|---|---|
| 백준 No.5670 [휴대폰 자판] (0) | 2022.04.02 |
| 백준 No.1708 [볼록 껍질] (0) | 2022.03.26 |
| 백준 No.11400 [단절선] (0) | 2021.08.29 |
| 백준 No.3190 [뱀] (0) | 2021.08.26 |




댓글