Baekjoon Online Judge No.11049 [행렬 곱셈 순서]
Problem
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
int N;
vector<PII> matrix_input;
PII matrixMul(PII& A, PII& B) {
return PII(A.first, B.second);
}
int cal(PII& A, PII& B) {
return A.first * A.second * B.second;
}
int findMin(vector<vector<int>>& dp, vector<vector<PII>>& matrix, int i, int j) {
int ans = INT_MAX;
for (int k = i; k < j; k++) {
if (k != i && k != j - 1) // dp[i][k], dp[k + 1][j], A[i][k] * A[k + 1][j]
ans = min(ans, dp[i][k] + dp[k + 1][j] + cal(matrix[i][k], matrix[k + 1][j]));
else // k == i || k == j - 1
if (k == i)
ans = min(ans, dp[k + 1][j] + cal(matrix_input[i], matrix[k + 1][j]));
else // k == j - 1
ans = min(ans, dp[i][k] + cal(matrix[i][k], matrix_input[j]));
}
return ans;
}
int solve() {
vector<vector<int>> dp;
vector<vector<PII>> matrix; // matrix[i][j] = input[i] ~ A[j] 까지 곱한 행렬의 row, col
matrix.assign(N, vector<PII>(N, PII(0, 0)));
for (int i = 0; i < N; i++)
for (int j = i + 1; j < N; j++)
matrix[i][j] = matrixMul(matrix_input[i], matrix_input[j]);
dp.assign(N, vector<int>(N, 0));
for (int j = 1; j < N; j++) {
for (int i = 0; i < N - j; i++) {
if (j == 1) {
dp[i][i + j] = cal(matrix_input[i], matrix_input[i + j]);
continue;
}
dp[i][i + j] = findMin(dp, matrix, i, i + j);
}
}
return dp[0][N - 1];
}
int main() {
cin >> N;
matrix_input.assign(N, PII(0, 0));
for (int i = 0; i < N; i++) {
int row;
int col;
cin >> row >> col;
matrix_input[i] = PII(row, col);
}
cout << solve();
}
|
cs |
How to solve
입력되는 행렬들은 vector<pair<int, int>> 로 받았다.
- matrix_input[ k ] == pair<int, int>(row_size_of_k'th_matrix, col_size_of_k'th_matrix)
Variables
- #35 _ vector<vector<int>> dp;
- #36 _ vector<vector<PII>> matrix;
#35
dp[ i ] [ j ] 는 matrix_input[ i ] 행렬부터 matrix_input[ j ] 행렬까지의 최소 곱셈 연산 수이다.
#36
matrix[ i ] [ j ] 는 matrix_input[ i ] 행렬부터 matrix_input[ j ] 행렬까지 곱했을 때 의 행의 길이, 열의 길이이다. #40 ~ #42 번째에서 값을 설정해준다.
- matrix[ i ][ j ].firist == row_size of matrix[ i ][ j ]
- matrix[ i ][ j ].second == column_size of matrix[ i ][ j ]
Functions
- #10 _ PII matrixMul(PII& A, PII& B);
- #14 _ int cal (PII& A, PII& B);
- #18 _ int findMin(vector<vector<int>>& dp, vector<vector<PII>>& matrix, int i, int j);
- #34 _ int solve()
#10
두 행렬을 입력받은 후, 곱한 후의 행렬을 return 한다. 이 문제에서 행렬이라 하면 pair<int, int>(row_size, col_size) 를 의미한다.
#14
두 행렬을 입력받은 후, 곱할 때 곱셈의 연산 횟수를 return 한다.
#18
dp[ i ][ j ]의 값을 구해주는 함수이다. 구해지는 원리의 예시를 위해 아래 사진을 첨부하였다.

dp[0][4]는 matrix_input vector 의 0번째 행렬부터 4번째 행렬까지 곱하면서 최소 곱셈 연산 횟수가 입력된다. 아래 4개의 case 들이 dp[0][4]의 후보가 된다. 즉, 최솟값이 저장되어야 하므로 min(case1 ~ case4)를 구해야 한다. for문을 돌려가면서 #23, #26, #28 처럼 ans 의 값을 min 값으로 계속해서 초기화를 시켜준다.
4개의 case 들 모두 두 개의 블록으로 나누어져 있다. case1의 왼쪽 블록, case4의 오른쪽 블록을 제외하곤 그 블록에 대한 dp[ i ][ j ]값은 이미 구해져 있는 상태이다. 즉 case마다 이미 구해져있는 dp값에 두 블록을 연결하면서 (두 행렬을 곱하면서) 드는 곱셈의 연산 횟수를 더해주면 구하고자 하는 dp[0][4]값이 된다.
- case 1) = A[0] * A[1][4] 의 곱셈 연산 횟수 + dp[1][4] // #26
- case 2) = A[0][1] * A[2][4] 의 곱셈 연산 횟수 + dp[0][1] + dp[2][4] // #23
- case 3) = A[0][2] * A[3][4] 의 곱셈 연산 횟수 + dp[0][2] + dp[3][4] // #23
- case 4) = A[0][3] * A[4] 의 곱셈 연산 횟수 + dp[0][3] // #28
이 식들을 일반화하면 아래의 식과 같다.
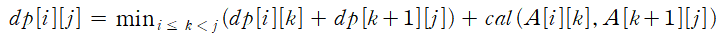
#34
아래 그림처럼 사선으로 DP를 하게 된다.

비어있는 칸은 고려하지 않는 칸들이다. 위에 써있는 순서대로 계산을 해 나간다. #46 ~ #55가 직접적인 계산을 하는 부분이다. 위 그림을 예시로 들 때 #48 ~ #51에선 dp[ k ][ k + 1 ]을 구해주게 된다. DP에 필요한 점화식의 초기값들을 메모이제이션 해주는 것으로, 복잡한 연산 없이 결국 두 행렬만 곱할때의 곱셈 연산 횟수를 넣어주면 되기 때문에 간단하다.
사선으로 DP를 진행하기 위한 nested for loop는 아래와 같은 형태로 짰다.

- i 의 값은 항상 0 부터 시작하고, 끝나는 값은 col - 1 부터 시작해서 계속해서 1씩 줄어든다.
- j 의 값은 시작값은 1부터 시작해서 계속해서 1씩 커지고 끝나는 값은 항상 row - 1 값이다.
이때 줄어들고 늘어난다의 기준은, 위 <사선 DP> 그림에서 화살표가 끝나고 다음 화살표가 시작될 때이다. 즉, nested for loop 가 한바퀴 한바퀴 돌 때 값이 변한다는 의미이다.
'Algorithm (C++ based) > BOJ' 카테고리의 다른 글
| 백준 No.10942 [팰린드롬?] (0) | 2021.02.05 |
|---|---|
| BOJ No.2798 [블랙잭] (0) | 2021.02.05 |
| 백준 No.1912 [연속합] (0) | 2021.02.02 |
| 백준 No.2603 [색종이 만들기] (0) | 2021.01.24 |
| 백준 No.2447 [별 찍기 - 10] (0) | 2021.01.24 |




댓글