
BOJ No.1167 [트리의 지름]
문제
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
설명
<알고리즘 분류>
* Tree
* DFS

트리의 지름이란, 트리 상에서 가장 먼 거리를 가지는 두 정점 사이의 경로이다. 위 예시 트리에서 H 노드와 G 노드 사이의 거리는 23이며, 이 경로가 트리의 지름이 된다.
트리의 지름은 다음과 같은 순서로 구해진다.
1. DFS를 통해 임의의 정점(x)으로부터 가장 먼 정점(y)을 구한다.
2. DFS를 통해 구해진 (y)정점으로부터 가장 먼 정점(z)를 구한다.
3. (y) 정점과 (z) 정점을 잇는 경로가 트리의 지름이 된다.
[증명]
(y) 정점과 (z) 정점을 잇는 경로가 트리의 지름이 된다는 것은 트리상에서 임의의 정점(x)으로부터 가장 멀리 떨어져 있는 정점 (y) 는 항상 지름의 양 끝중 한 곳에 존재한다는 의미이다. 이는 "(y) 정점은 트리의 지름에 포함되지 않는다" 라는 말은 모순이 된다는 것을 보임으로써 증명할 수 있다.
(y) 정점이 트리의 지름에 포함되지 않는 경우는 아래와 같은 경우들이 된다. 아래 경우들이 전부 모순임을 증명할 수 있다. 아래 예시들은 임의의 정점 (x)로부터 가장 먼 정점 (y) 이며, (u) 정점과 (v) 정점을 연결하는 경로가 트리의 지름인 경우에 해당된다. 또한 d(a, b)는 (a) 정점과 (b) 정점 사이의 거리를 나타낸다.
(1) (x) 정점과 (u) 정점이 겹치는 경우
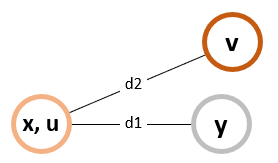
이러한 경우에는 결국 d(x, y) == d(u, v) 가 된다. (x) 정점 으로부터 가장 멀리 있는 정점 (y) 이지만, (x) 정점은 결국 (u) 정점과 동일한 정점 이기 때문이다. 즉, d1 == d2 이며 (y) 정점은 (v) 정점과 겹치거나 (x) 정점 으로부터 같은 거리에 있는 정점이 된다.
(2) (x)---(y) 경로와 (u)---(v) 경로의 일부가 겹치는 경우
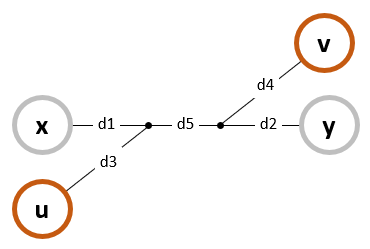
(x) 정점에서 가장 먼 정점은 (y) 정점 이다. 즉, d4 =< d2가 성립되어야 한다. 하지만 트리의 지름은 d3 + d5 + d4 에 해당된다. 즉, d2 == d4 혹은 (y) 정점 == (v) 정점이 성립되어야 위 경우가 성립될 수 있다.
(3) (x)---(y) 경로와 (u)---(v) 경로가 서로 독립적인 경우

(x) 정점에서 가장 먼 정점은 (y) 정점 이라는 점에서, d5 + max(d3, d4) =< d2 가 성립되어야 한다. 또한 이 가정이 성립되기 위해선 d2 == d5 + max(d3, d4) 혹은 (y) 정점 == (u) 정점 or (v) 정점이어야 한다.
위 경우들을 통해, (y) 정점 는 (u) 정점 혹은 (v) 정점 과 겹치거나 (y) 정점 가 (u) 정점, (v) 정점 와 겹치지 않더라도 (y) 정점 가 포함된 트리의 지름의 길이는 (u) 정점, (v) 정점 로 이루어진 트리의 지름의 길이와 동일하다는 것을 확인할 수 있다.
<정리>
1. 위 방법에 대한 증명은 귀류법으로 진행되었다.
2. 설령 (y) 정점가 (u) 정점, (v) 정점 과 겹치지 않더라도 (y) 정점가 포함된 지름의 길이는 (u) 정점, (v) 정점 으로 이루어진 지름의 길이와 같다.
Code
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
typedef pair<int, int> pii;
int n;
int maxVal = 0;
int maxNode = 0;
vector<pii> nodes[100001];
bool visit[100001];
void dfs(int bef, int cur, int val = 0) {
visit[cur] = true;
if (maxVal < val) {
maxVal = val;
maxNode = cur;
}
for (int i = 0; i < nodes[cur].size(); i++) {
int nxt = nodes[cur][i].first;
if (!visit[nxt])
dfs(cur, nxt, val + nodes[cur][i].second);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> n;
int cur = 0;
int nxt = 0;
int dis = 0;
for (int i = 1; i <= ::n; i++) {
cin >> cur;
while (cin >> nxt && nxt != -1) {
cin >> dis;
nodes[cur].push_back(pii(nxt, dis));
}
}
dfs(0, 1);
memset(visit, false, 100001);
dfs(0, maxNode);
cout << ::maxVal;
}'Algorithm (C++ based) > BOJ' 카테고리의 다른 글
| 백준 No.1967 [트리의 지름] (0) | 2022.11.28 |
|---|---|
| 백준 No.1725 [히스토그램] (2) | 2022.11.13 |
| 백준 No.10986 [나머지 합] (0) | 2022.04.19 |
| 백준 No.1019 [책 페이지] (0) | 2022.04.13 |
| 백준 No.5670 [휴대폰 자판] (0) | 2022.04.02 |




댓글