
BOJ No.10986 [나머지 합]
문제
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
설명
<알고리즘 분류>
* 구간 합 (Prefix sum)
구간 합을 간단하게 활용 한 문제이다.
참고 Link : 2022.04.19 - [Algorithm (C++ based)/Algorithm 이론] - 구간 합 (Prefix sum)
만약 4번째 원소 (index == 3) 부터 19번째 원소 (index == 18) 까지 구간 합이 m 으로 나누어 떨어진다면?
sum[k] 를 index == k 인 원소까지의 누적 합 이라고 할 때,
sum[2] % m == sum[18] % m 이라는 식이 성립하게 된다면 index 구간 3 ~ 18 에 해당되는 원소들의 구간 합은 m 으로 나누어 떨어지게 된다.
아래 코드에서 arr 배열에 대한 설명은! 예시로 arr[k] 의 값은 index == k 인 원소까지의 누적 합을 m으로 나눈 나머지 값이 k 인 원소에 해당된다.
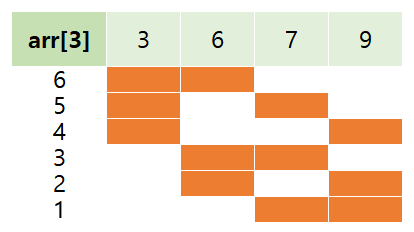
누적 합을 m 으로 나눴을 때 나머지가 3인 원소들의 index 를 넣은 배열을 예시 들어봤다. 위와 같은 경우 주황색들과 같이 선택이 되면서 구간합을 m 으로 나눴을 때 0이 되는 경우들을 확인할 수 있다. arr[k] 의 원소의 개수가 C 개라고 할 때 이 arr[k] 에서 구현할 수 있는 값은 (C - 1) 가 되므로 정답에 (C - 1)! 의 값이 더해지는 것 이다.
단, 체크해야 할 게 있다. arr[0] 의 경우에는 arr[0] 에 적힌 두 원소의 조합 이외에도 혼자만으로도 정답이 될 수 있다. 따라서 arr[0] 의 경우에만 C! 의 값이 더해진다.
<정리>
1. 누적 합을 이용하여 구간 합의 나머지를 구할 것 이다.
2. 누적 합을 m 으로 나눈 나머지의 값을 기준으로 배열을 나눈다.
3. 누적 합의 나머지의 값이 같은 원소들은 서로의 조합으로 구간 합을 m 으로 나눈 나머지의 값이 0이라는 정답을 낸다.
4. 단, 누적 합의 나머지의 값이 0인 원소들은 혼자만으로도 정답이 된다.
Code
#include <iostream>
#include <vector>
using namespace std;
typedef unsigned long long ull;
vector<int> arr;
int n;
ull m;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
arr.assign(m, 0);
ull cur;
ull sum = 0;
ull ans = 0;
for (int i = 0; i < n; i++) {
cin >> cur;
sum += cur;
ans += arr[sum % m]++;
}
cout << ans + arr[0]; // 나머지가 0인 집합들은 혼자만 있어도 가능하므로
}'Algorithm (C++ based) > BOJ' 카테고리의 다른 글
| 백준 No.1725 [히스토그램] (2) | 2022.11.13 |
|---|---|
| 백준 No.1167 [트리의 지름] (3) | 2022.07.13 |
| 백준 No.1019 [책 페이지] (0) | 2022.04.13 |
| 백준 No.5670 [휴대폰 자판] (0) | 2022.04.02 |
| 백준 No.7420 [맹독 방벽] (0) | 2022.03.28 |




댓글