힙 (Heap), 최대힙/최소힙
정의
힙(Heap) 이란 완전이진트리(Perfect Binary Tree) 를 응용한 자료구조이다. 완전이진트리는 아래와 같은 Binary Tree를 의미한다.

완전이진트리는, 위처럼 마지막 레벨을 제외하면 모두 포화상태이며 마지막 레벨에 해당되는 노드들은 모두 좌측으로 쏠려있는 Binary Tree 이다.
이를 이용해서 힙(Heap)이라는 자료구조에 접근을 할 수 있다. 예를 들어 만약 최소힙을 생성하게 되면, Parent node 는 항상 Child node 보다 작거나 같은 값을 가지게 된다.
설명
힙(Heap)은 일반적으로 어떠한 수의 배열에 있어서 최소값과 최대값을 구할 때 쓰인다. 최소값을 구할 때 쓰이는 힙(Heap)은 최소힙(Min Heap) 이라고 불리고 최대값을 구할 때 쓰이는 힙은 최대힙(Max Heap) 이라고 불린다.

위의 정수 array 에서 최소/최대값을 구하려고 한다. 완전탐색으로 array를 탐색하여 최소/최대값을 구한다면 이 array를 선형적으로 모두 탐색을 하게 되고 O(N)의 Time complexity 를 가진다. 그리고 array 에서 최소값 혹은 최대값을array 에서 삽입 및 삭제하는 작업을 한 후 다시 최소값, 최대값을 찾는 작업 또한 O(N)의 Time complexity를 가진다. 사이즈가 굉장히 큰 array에 대해서 이러한 선형적인 방법으로 최소/최대값을 탐색한다면 굉장히 비효율적일 것 이다.
그래서 최소힙/최대힙을 통해 더 빠르게 최소값과 최대값에 대해서 더 빠르게 처리할 수 있다. 최소힙과 최대힙을 구현하는 작업은 O(N) 복잡도보다 빠르게 되는 것이 아니지만 (혹시 O(N) 보다 빨리 구현되는 방법이 있다면 연락 주시면 감사드리겠습니다), 구현한 최소힙과 최대힙을 활용을 한다면 array 원소의 삽입/삭제에 대해서 최소값과 최대값을 다시 재정의하는 작업은 Binary Tree를 응용한 알고리즘 답게 O(logN) 의 복잡도가 소요가 된다.
위 array 를 가지고 완전이진트리를 아래와 같이 정의할 수 있다.

각 노드마다 아래에 있는 숫자는 해당 노드의 번호를 의미한다. 한번 이를 가지고 최대힙을 구현해보자. 최대힙이 구현된 후에는 첫 번째 노드인 루트 노드에 이 array의 원소에서 가장 최대값이 대입이 되어있을 것 이다.
Parent Node 번호 : curNode
Left Child Node 번호 : 2 * curNode
Right Child Node 번호 : 2 * curNode + 1
최대힙을 만드는 과정은, array의 첫 번째 원소를 Root Node 에 두면서 시작한다.




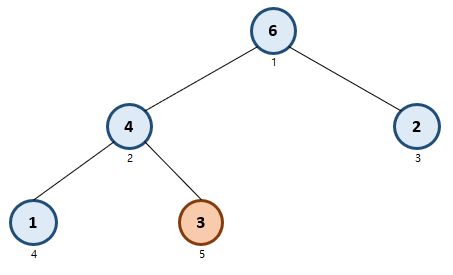



마지막 Node 까지 이 작업을 계속 하면 최종적으로 아래와 같은 최대힙이 구현이 된다.
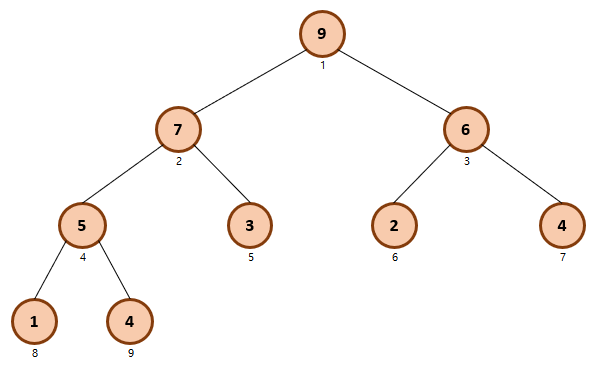
최종적으로 구현이 된 최대힙 Binary Tree 이다. 임의의 Parent Node 와 Child Node 의 관계를 보면, 모든 Parent node 들은 본인의 Child Node 들 보다 큰 것을 확인할 수 있다. 최소힙은 그냥 구현하는 과정에서, 최대힙을 구현하는 과정과 반대로 Parent Node 가 Child Node 보다 큰 경우 두 Node 를 Swap하면 된다.
이러한 최소힙/최대힙을 통해서 원소(노드)의 삽입이나 삭제를 한 후 최소값/최대값을 다시 구하는 과정을 O(logN) 시간복잡도를 가지고 할 수 있다. 또한 최소힙과 최대힙을 같이 활용하여 효율적인 중간값 관리를 할 수도 있다. (맨 아래 해당 링크가 첨부되어 있다)
Code
#include <iostream>
#include <vector>
using namespace std;
void heapify (vector<int>& minHeap, int curNode) {
if (curNode == 1) { // Root Node 인 경우
return;
}
else { // Root Node 가 아닌 경우
while (curNode / 2) { // Parent Node 가 존재하는 경우
int parentNode = curNode / 2;
// Child Node 가 더 크면 Swap
if (minHeap[parentNode] < minHeap[curNode]) {
int temp = minHeap[parentNode];
minHeap[parentNode] = minHeap[curNode];
minHeap[curNode] = temp;
}
curNode /= 2;
}
}
}
int main() {
int n;
cin >> n;
int heapSize = 0;
vector<int> minHeap(4 * n, 0);
for (int i = 1; i <= n; i++) {
int num; cin >> num; // 원소를 차례대로 입력
minHeap[++heapSize] = num;
heapify(minHeap, heapSize);
}
for (int i = 1; i <= n; i++)
cout << minHeap[i] << ' ';
}Link
- 최소힙/최대힙 에서 Node 삽입 및 삭제 : 2021.07.22 - [C++/Data structure] - 힙[Heap], 삽입 및 삭제
- 중간값 관리 (백준 No.1655 [가운데를 말해요]) : // 작성중
- 최소힙 (백준 No.1927 [최소 힙]) : // 작성중
- 최대힙 (백준 No.11279 [최대 힙]) : // 작성중
'C, C++ > Data structure' 카테고리의 다른 글
| 이진 트리 (Binary Tree) (0) | 2023.01.14 |
|---|---|
| 세그먼트 트리 (Segment tree) (0) | 2021.08.03 |
| 힙[Heap], 삽입 및 삭제 (1) | 2021.07.22 |
| Bitmask (2), "자주 사용되는 형태" (0) | 2021.02.25 |
| Bitmask (1), "Bit operator" (0) | 2021.02.09 |




댓글