// Baekjoon Online Judge No.10757 [큰 수 A+B]
Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int main() {
string A, B;
bool AisLonger = false;
bool BisLonger = true;
cin >> A;
cin >> B;
int maxLen = B.length();
int minLen = A.length();
if (A.length() > B.length()) {
maxLen = A.length();
minLen = B.length();
AisLonger = true;
BisLonger = false;
}
vector<int> sum;
int olim = 0;
for (int i = 1; i <= maxLen; i++) {
if (i <= minLen) {
sum.push_back((A[A.length() - i] + B[B.length() - i] - 96 + olim) % 10);
olim = (A[A.length() - i] + B[B.length() - i] - 96 + olim) / 10;
}
else if (AisLonger) {
sum.push_back((A[A.length() - i] - 48 + olim) % 10);
olim = (A[A.length() - i] - 48 + olim) / 10;
}
else { // B is longer than A
sum.push_back((B[B.length() - i] - 48 + olim) % 10);
olim = (B[B.length() - i] - 48 + olim) / 10;
}
if (i == maxLen) {
if (olim) sum.push_back(olim);
}
}
for (int i = sum.size() - 1; i >= 0; i--) {
cout << sum[i];
}
}
|
cs |
시행착오
이 문제에서 눈여겨보아야 할 것은 입력조건이다. A와 B의 값이 10^10,000 미만인 값까지 입력이 가능해야 하는데, 자료형중 가장 큰 수를 표현할 수 있는 자료형인 double 조차도 약 1.7 * 10^308 까지밖에 표현을 하지 못한다.

이는 C++에서 덧셈에 대한 새로운 시각을 요구하는 문제였다. 단순하게 생각해서 overflow가 되는 횟수를 count해서 풀어야하나? 라는 생각을 했지만 이내 접었다.
첫번째로 생각한 방법은 int형 vector를 선언하여 input되는 한자리 한자리 수를 vector에 넣는 것 이었다. 실제로 가능한 방법이긴 하지만 수의 길이만큼 vector에 하나하나 push_back을 해 주어야 하기 때문에 효율적이지 못할 것이라고 생각하였다. 만약 수의 크기가 10^10,000에 육박하는 크기라면 많은 시간이 걸릴 것이기 때문이다. 또한 A와 B를 더해야 하니 시간이 더 소요가 될 거라고 생각을 했다. 그래서 생각해낸 방식이 input을 문자열로 받는 것이었다.
How to solve
두 개의 input을 string의 형태로 받고, vector<int> sum에 첫 번째 자리 수부터 더해진 값이 push_back되어 실제 덧셈이 되는 과정처럼 덧셈을 진행하는 코드를 구현하였다.
|
12
13
|
cin >> A;
cin >> B;
|
cs |
A와 B를 string형태로 입력받는다.
|
15
16
|
int maxLen = B.length();
int minLen = A.length();
|
cs |
우선 default 값으로 A, B중 더 긴 문자열을 B라고 둔다. 또한 이에 따라 B의 길이값으로 maxLen변수를 정의하였다. minLen은 A의 길이값이 되었다. 추후 A가 더 길면 maxLen에 A의 길이값, minLen에 B의 길이값을 넣으면 되기 때문이다. B가 더 길다고 우선 가정했기에 AisLonger변수는 false, BisLonger변수는 true로 정의한다.
|
18
19
20
21
22
23
|
if (A.length() > B.length()) {
maxLen = A.length();
minLen = B.length();
AisLonger = true;
BisLonger = false;
}
|
cs |
15 ~ 16번째 line에서 B의 길이가 더 길다고 가정하고 값을 부여하였었다.
18 ~ 23번째 line에선 A의 길이가 더 길 경우 maxLen과 minLen의 값을 다시 정의하고,
AisLonger = true, BisLonger = false 로 재정의 한다.
B가 더 길거나 A의 길이와 B의 길이가 같을 경우엔 그냥 전에 정의한 대로 둔다.
|
25
26
27
|
vector<int> sum;
int olim = 0;
|
cs |
25번째 line에선 결과값을 넣을 int형 vector를 선언하였다.
27번째 line에선 덧셈 과정에서 발생할 올림수의 기능을 하는 변수를 선언하였다.
|
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
for (int i = 1; i <= maxLen; i++) {
if (i <= minLen) {
sum.push_back((A[A.length() - i] + B[B.length() - i] - 96 + olim) % 10);
olim = (A[A.length() - i] + B[B.length() - i] - 96 + olim) / 10;
}
else if (AisLonger) {
sum.push_back((A[A.length() - i] - 48 + olim) % 10);
olim = (A[A.length() - i] - 48 + olim) / 10;
}
else { // B is longer than A
sum.push_back((B[B.length() - i] - 48 + olim) % 10);
olim = (B[B.length() - i] - 48 + olim) / 10;
}
if (i == maxLen) {
if (olim) sum.push_back(olim);
}
}
|
cs |
문제 풀이에 가장 핵심이 되는 부분이다. A, B 의 첫번째 자리 수는 A[0], B[0]이 아닌 A와 B의 마지막 글자의 값이라 for문을 i = 1부터 돌리면서 A[A.length() - i], B[B.length() - i]를 이용하여 연산을 진행하였다.
고려해야 할 요소들은 다음과 같다.
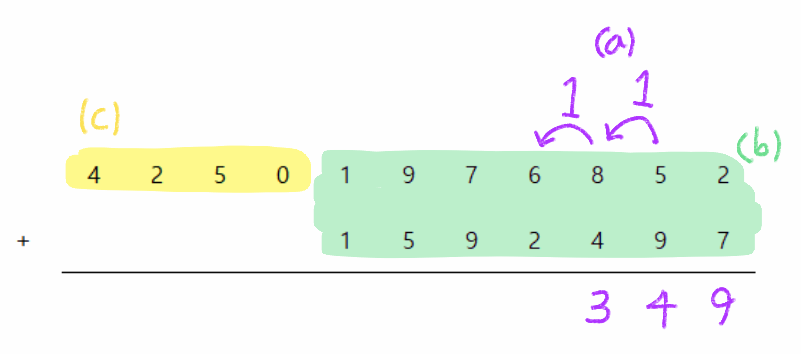
- (a) : 덧셈 과정에서 발생하는 올림수
- (b) : 두 수의 덧셈이 이루어지는 곳
- (c) : 짧은 수의 덧셈이 끝난 경우.
첫번째로, (a) 의 경우는 말 그대로 올림수에 대한 부분이다. for 문이 한자리 한자리 숫자를 더해가면서 이전 자리 수의 덧셈에서 발생한 올림수도 더해준다.
두번째로, (b) 의 경우는 더해야 할 요소가 세 가지가 있다. A의 숫자, B의 숫자, 그리고 올림수이다. 이 경우에 대한 조건식은 30번째 line이다. 코드를 보면 더해지는 숫자들에 -96, -48을 한 것을 볼 수 있는데 이는 처음에 입력을 string의 형태로 받았으므로 A[k], B[k]의 자료형은 char 이기에 char형태인 '0', '1' ... 의 ASCII코드 10진수 값이 48, 49 ... 임을 고려하여 넣은 뻴셈이다.
세번째로, (c) 의 경우는 짧은 수의 덧셈은 다 마무리가 되고 남아있는 긴 수와 올림수만 더해주면 된다. 34, 38번째 조건문에서 (c)의 과정을 수행한다. 34번째는 A가 B보다 길 경우, 38번째는 B가 A보다 길 경우이다.
sum vector에 push_back 되는 값은 한 자리 숫자여야만 한다. 다 더해진 값이 19라면 sum vector엔 첫째자리수인 9만 push_back되고 십의자리수인 1은 올림수로 다음 자리 수의 덧셈에 전달된다. 따라서 다 더한 값에 '% 10'을 해 준것을 볼 수 있다. olim은 당연히 '/ 10'을 해 주었다.
43번째 line에선 i == maxLen 일 경우 즉, 긴 수의 끝까지 덧셈을 실행했을때의 경우이다. 이 경우를 따로 빼놓은 이유는 마지막 자리의 덧셈에서 또 올림수가 발생했다면 sum 에 그 올림수까지 push_back을 해주어야 하기 때문이다.
|
48
49
50
|
for (int i = sum.size() - 1; i >= 0; i--) {
cout << sum[i];
}
|
cs |
A와 B의 덧셈에 대한 결과를 첫째자리수부터 push_back 했으므로 출력할땐 sum[0]부터가 아닌 sum[sum.size() - 1]부터 출력해야 한다. 따라서 for문의 범위가 이와 같다.
'Algorithm (C++ based) > BOJ' 카테고리의 다른 글
| 백준 No.2603 [색종이 만들기] (0) | 2021.01.24 |
|---|---|
| 백준 No.2447 [별 찍기 - 10] (0) | 2021.01.24 |
| 백준 No.10844 [쉬운 계단 수] (0) | 2020.11.18 |
| 백준 No.1932 [정수 삼각형] (0) | 2020.11.16 |
| 백준 No.1149 [RGB거리] (0) | 2020.11.10 |




댓글