위상 정렬 (Topological Sort)
위상정렬
위상정렬은 무향 비순환 그래프 (DAG : Directed Acylic Graph) 에서 정해진 순서에 맞게 나열을 하는 것 이다. 일상에서의 예시로 대학교 과목 이수도 에서 선수과목이 있는 것을 생각해 볼 수 있다.
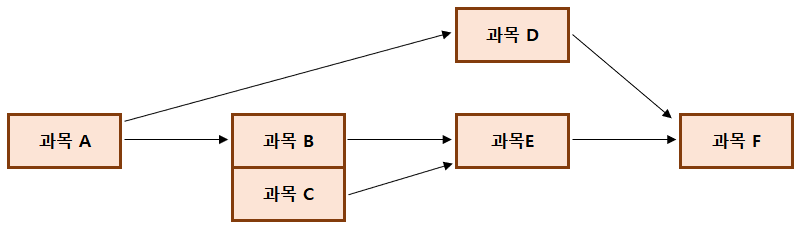
과목 F 를 듣기 위해선, 과목 D, E 를 들어야 한다. 또 과목 D를 듣기 위해선 과목 A를, 과목 E 를 듣기 위해선 과목 B, C 를 들어야 하고 과목 B를 듣기 위해선 과목 A를 들어야 한다. 이 경우 가장 처음에 들을 수 있는 과목은 선수과목이 없는 과목 A와 과목 C 이다. 위상 정렬은 이러한 선수과목이 없는 경우 즉, 진입 간선이 없는 경우를 따져가면서 정렬을 해 나가는 알고리즘 이다.
설명
1. 주어진 노드와 간선에 대한 정보들을 바탕으로 각 노드별로 진입 간선(inDegree)의 개수와 진출 간선(outDegree) 의 개수를 파악한다.
2. inDegree의 개수가 0인 노드들을 파악하고 queue 에 삽입한다. 초기에 inDegree의 개수가 0인 노드만 진입이 가능한 노드이기 때문이다.
3. queue 가 비어있지 않는 경우에 계속해서 queue 의 가장 앞에 있는 노드를 뽑은 후 그 노드의 outDegree 들을 파악하고, 그 outDegree 들 각각의 inDegree 개수를 하나씩 줄인다. outDegree 들 입장에서 현재 뽑힌 노드가 하나의 indegree 노드 이기 때문이다. 그리고, inDegree 개수를 줄임으로써 inDegree 의 개수가 0이 된 노드가 있다면 이 노드를 queue 에 삽입한다.
4. 위상 정렬이 된 1차원 배열을 얻어야 한다면 inDegree의 개수가 0인 노드가 탐색 될 때 마다 순서대로 배열에 삽입시키면 된다.
5. queue가 queue.empty() == true 가 되면 정렬을 다 마친 상태이다.
Code
더보기
#include <iostream>
#include <vector>
#include <queue>
#define SIZE 100
using namespace std;
vector<int> inDegree(SIZE + 1, 0);
vector<vector<int>> outDegree(SIZE + 1);
vector<int> sortedArray;
queue<int> q;
int vertex, edge;
void print() {
for (int i = 0; i < sortedArray.size(); i++)
printf(" array[%d] = %d\n", i, sortedArray[i]);
}
void solve() {
int cur, size, next;
while (!q.empty()) {
cur = q.front(); q.pop(); // queue 의 가장 앞 원소를 뽑는다.
sortedArray.push_back(cur);
size = outDegree[cur].size();
for (int i = 0; i < size; i++) {
next = outDegree[cur][i];
if (--inDegree[next] == 0)
q.push(next);
}
}
}
void init() {
cin >> vertex >> edge;
int s, e;
for (int i = 1; i <= edge; i++) {
cin >> s >> e;
inDegree[e]++;
outDegree[s].push_back(e);
}
for (int i = 1; i <= vertex; i++)
if (inDegree[i] == 0)
q.push(i); // 진입 간선의 수가 0인 노드를 queue 에 삽입
}
int main() {
init();
solve();
print();
}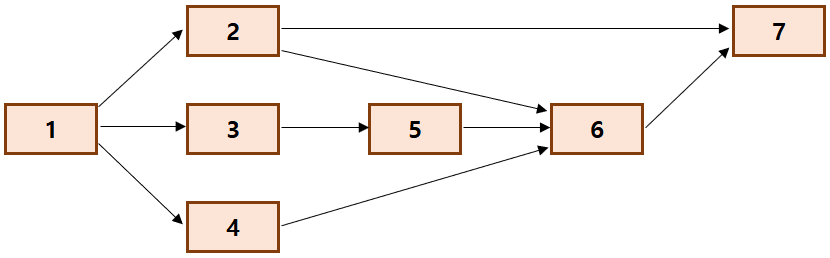
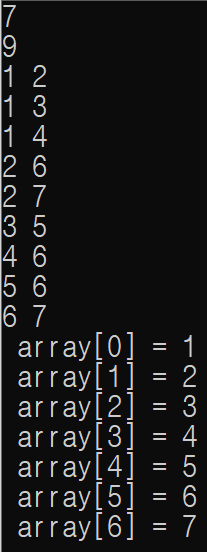
위 그래프로 위상 정렬을 진행을 해 보았다.
결과
728x90
'Algorithm (C++ based) > Algorithm 이론' 카테고리의 다른 글
| 최소 스패닝 트리 / 최소 신장 트리 (MST) (0) | 2021.08.09 |
|---|---|
| 유니온 파인드 (Union Find, Disjoint set) (0) | 2021.08.06 |
| 투 포인터 알고리즘 (Two pointer Algorithm) (0) | 2021.07.20 |
| 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2021.02.20 |
| Dijkstra (다익스트라) (0) | 2021.02.08 |




댓글