Dijkstra
What is Dijkstra?
그래프의 한 노드에서 다른 노드로 갈 때 드는 가중치들의 합의 최소값을 구하는 알고리즘이다. 이 '가중치'를 문제가 요구하는 바에 따라 거리, 비용 등의 형태로 문제에 다양하게 적용시킬 수 있을 것 같다.
Explanation
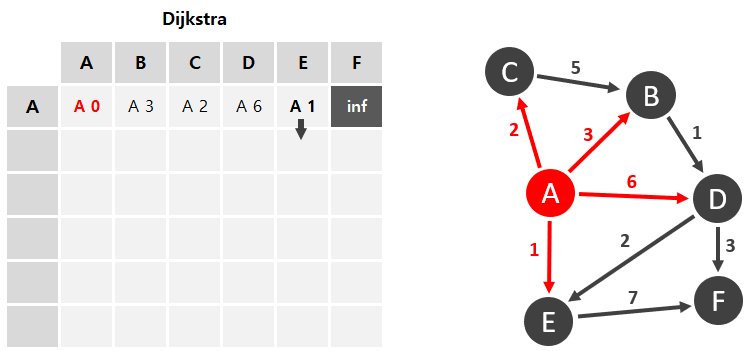
A정점부터 탐색을 시작해봤다. 실제 코드에서 알고리즘을 사용할 땐 처음에 시작하고자 하는 정점을 정해주면 된다. 좌측의 표에서 빨간색은 확정된 최소 비용을 나타낸다. A에서 A로 갈 때에는 당연히 비용이 0이므로 확정이다. 숫자 앞에 A를 붙인 이유는 직전에 A에서 왔다는 의미이다. B, C, D E 열에 차례대로 비용을 적어준다. F열은 A에서 F로 가는 간선이 없으므로 inf 라고 하자. 저렇게 나열해준 뒤 확정이 된 빨간색 칸을 제외하고 B ~ F 정점들 중 가장 작은 비용을 가지고 있는 정점을 다음 정점으로 (아래 행) 내린다. 위 상황에선 E정점이 1의 가중치로 제일 작으므로 다음 행으로 E정점을 탐색한다.
우측 그래프에서 빨간색은, 좌측 표의 빨간색과 무관하며 그냥 현재 탐색하고 있는 정점 밑 간선을 나타내 보았다.
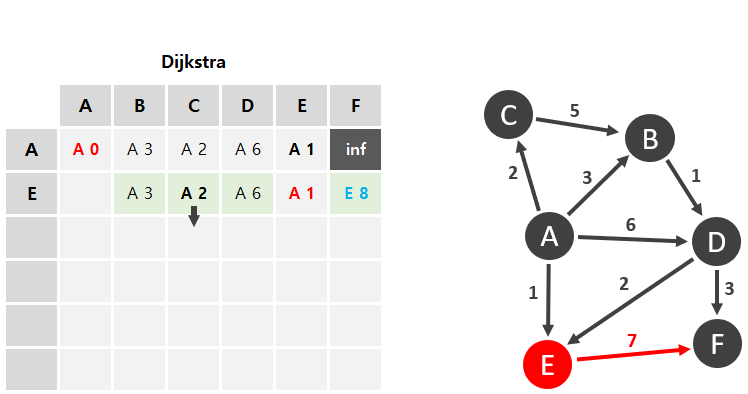
이어서 내린 값인 A 1은 A에서 E로 가는 확정 최소 비용이므로 빨간색으로 해 주었다. 증명(?)을 좀 하자면 만약 최소 비용이 아니려면 A에서 E가 아닌 다른 정점을 거쳐 E로 오는 비용이 최소 비용인 경우일텐데 애초에 A정점에서 E정점으로 오는게 B ~ F 정점들중 가장 적은 비용이므로 다른 정점을 거쳐서 E에 도착하는 비용은 무조건 1보다 클 수밖에 없다.
연두색 칸들은 두 가지 경우에 의해 결정이 된다.
- 현재 탐색하는 정점을 거치고 가는게 더 최소 비용인지
- 아니면 현재 탐색중인 정점은 무시하고 이전에 갔던 대로 가는게 더 최소 비용인지
E행 F열은 칸은 이전에 A--F 간선이 없는 바람에 inf값을 가졌으므로 E를 거쳐서 F에 가는게 최소비용이 된다. 따라서 (A에서 E를 가는데 확정된 최소 비용 + E에서 F가는 비용) 인 8을 넣어주었다. 직전에 E에서 왔으므로 E를 앞에 붙여주었다. 나머지 다른 세 개의 연두색 칸들은 위 조건에 따라 그냥 이전에 값이 적어졌다. 그리고 이전과 같은 원리로 제일 작은 값인 2를 갖고있는 C정점을 다음 행으로 내려준다. 그 후 지금까지 설명한 방식대로 쭉쭉 써내려간다.



이 경우엔 A에서 F로 가는 비용이 이전 A--E--F 을 통해서 온 8보다 A--B--D--F 를 통해서 온 7이 더 적으므로 D 7을 적어주었다.

마지막 행까지 채워지면서, 각 정점에 가기 위한 최소 비용을 전부 구하게 되었다.
- 시간 복잡도 : O(E logV)
Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#include <iostream>
#include <vector>
#include <queue>
#define cost first
#define vertex second
using namespace std;
typedef pair<int, int> PII;
const int INF = 2100000000;
int V, E;
int K;
vector<vector<PII>> node;
vector<int> solve(int K) {
vector<int> cost_to(V + 1, -1); // cost[i] == (K) ---> (i) 's min cost
priority_queue<PII, vector<PII>, greater<PII>> pq;
// first = cost, second = vertex_pos
cost_to[K] = 0;
pq.push(PII(cost_to[K], K));
while (!pq.empty()) {
int curVer = pq.top().vertex;
int curCost = pq.top().cost;
pq.pop();
if (curCost > cost_to[curVer]) continue;
for (int i = 0; i < node[curVer].size(); i++) {
int nextVer = node[curVer][i].vertex;
int nextCost = curCost + node[curVer][i].cost;
if (cost_to[nextVer] == -1 || cost_to[nextVer] > nextCost) {
cost_to[nextVer] = nextCost;
pq.push(PII(nextCost, nextVer));
}
}
}
return cost_to;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> V >> E;
cin >> K;
node.resize(V + 1);
for (int i = 0; i < E; i++) {
int s, e, v;
cin >> s >> e >> v;
node[s].push_back(PII(v, e));
}
vector<int> answer = solve(K);
for (int i = 1; i < answer.size(); i++) {
if (answer[i] != -1) cout << answer[i] << '\n';
else cout << "INF" << '\n';
}
}
|
cs |
'Algorithm (C++ based) > Algorithm 이론' 카테고리의 다른 글
| 위상 정렬 (Topological Sort) (0) | 2021.08.05 |
|---|---|
| 투 포인터 알고리즘 (Two pointer Algorithm) (0) | 2021.07.20 |
| 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2021.02.20 |
| Palindrome (팰린드롬) (0) | 2021.02.05 |
| Greedy algorithm (탐욕 알고리즘) (0) | 2020.11.10 |




댓글