플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
What is Floyd-Warshall Algorithm?
Dijkstra (다익스트라) 알고리즘이 시작하고자 하는 한 vertex에서 나머지 vertex들로 가는 최소 비용을 구하는 알고리즘 이라면, 플로이드 워셜 알고리즘(Floyd-Warshall Algorithm)은 모든 정점에서 모든 정점으로 가는 최소 비용을 2차원 array 혹은 vector 에 저장을 해 둔다. 아래 코드에선 floyd[ i ][ j ]로 표기했고, 이 의미는 vertex i 에서 vertex j 로 가는 최소 비용을 의미한다. floyd[ i ][ j ]의 값을 vertex i, vertex j 를 제외한 모든 vertex 를 경유해보면서 더 작은값을 계속해서 갱신한다. 점화식을 사용하므로 Dynamic programming 이다. 사용되는 점화식은 아래와 같다.

Explanation
|
1
2
3
4
5
6
7
8
9
10
11
|
floyd.assign(V + 1, vector<ull>(V + 1, INF));
for (int visit = 1; visit <= V; visit++) {
for (int i = 1; i <= V; i++) {
for (int j = 1; j <= V; j++) {
if (i != visit && j != visit) {
floyd[i][j] = min(floyd[i][j], floyd[i][visit] + floyd[visit][j]);
}
}
}
} |
cs |
- 첫 번째 for문 에서 경유하고 갈 vertex를 지정한다.
- 두 번째, 세 번째 for문 에서 모든 edge를 점검하고 갱신한다. 이 때, vertex i 그리고 vertex j 는 경유하는 vertex visit과는 다른 vertex 이어야 한다. #6 line 의 조건문이 이에 해당한다.
총 3중 for문이 vertex 1 부터 마지막 vertex 까지 돌아가므로, 시간복잡도는 O(V^3) 이다.
아래 Floyd-Warshall 이 진행되는 형태를 직관적으로 나타내 보았다.



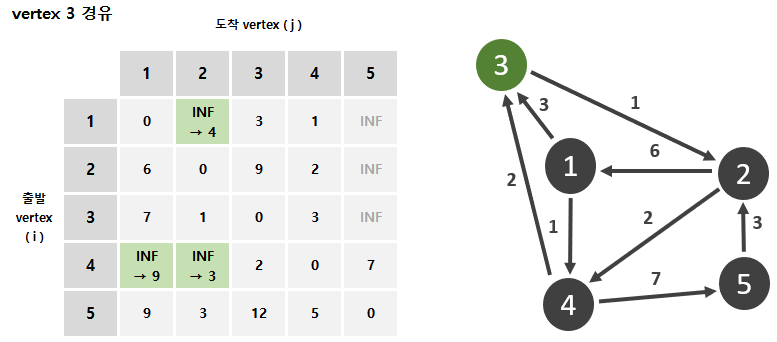
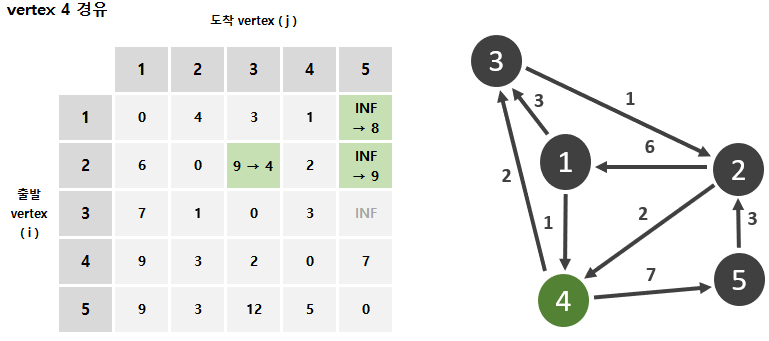
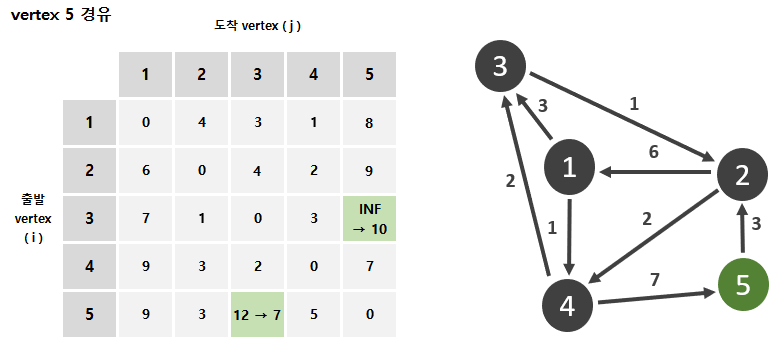
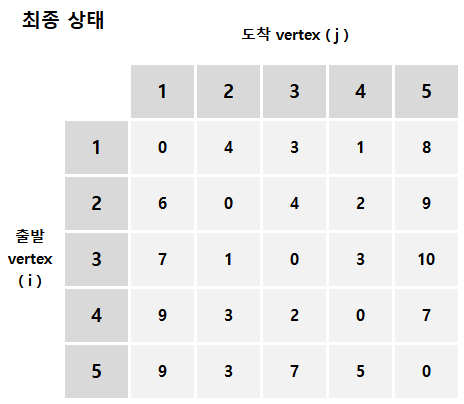
728x90
'Algorithm (C++ based) > Algorithm 이론' 카테고리의 다른 글
| 위상 정렬 (Topological Sort) (0) | 2021.08.05 |
|---|---|
| 투 포인터 알고리즘 (Two pointer Algorithm) (0) | 2021.07.20 |
| Dijkstra (다익스트라) (0) | 2021.02.08 |
| Palindrome (팰린드롬) (0) | 2021.02.05 |
| Greedy algorithm (탐욕 알고리즘) (0) | 2020.11.10 |




댓글