구간 합 (Prefix sum)
array 에서 누적 합을 통해 구간 합을 구할 수 있다.
정의
Array 에서 누적 합을 통해 원하는 구간의 합을 구할 수 있다.
설명
1차원 Array 에서의 구간 합

arr Array 는 1차원 배열이고, sum Array 는 0 번째 index 를 가지는 원소부터 그 index 값의 원소까지의 누적 합 배열이다.

위와 같이 3번째(index == 2) 원소 부터 7번째(index == 6) 원소 까지의 구간 합을 구하고 싶으면?

sum[6] - sum[1] 을 하면 구할 수 있다 ;)
관련 Code
sum[0] = arr[0];
for (int i = 1; i < n; i++) {
sum[i] += sum[i - 1] + arr[i];
}
// 6 ~ 17 번째 원소들의 구간 합은?
cout << " The answer is " << sum[16] - sum[4];
이러한 원리를 이용한 구간 합은 n차원 Array 에서도 구할 수 있다.
2차원 Array 에서의 구간 합

2차원 Array가 있고, sum Array 는 구간 합 Array 이다. arr[0][0] 부터 arr[i][j] 까지의 합이 sum[i][j] 에 기입 되어있다.
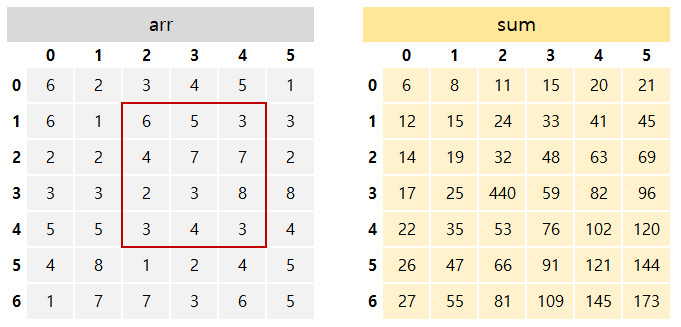
위 영역에 해당되는 구간 합을 구하려면?
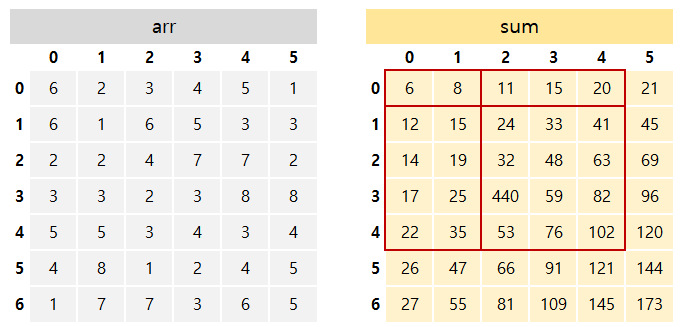
sum[4][4] - sum[4][1] - sum[0][4] + sum[0][1] 의 값을 구해주면 된다.
관련 Code
for (int i = 0; i < r; i++)
for (int j = 0; j < c; j++) {
cin >> arr[i][j];
if (i == 0 && j == 0) sum[0][0] = arr[0][0];
else if (i == 0 && j) sum[i][j] = sum[i][j - 1] + arr[i][j];
else sum[i][j] = arr[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
}
// (4, 5) ~ (11, 12) 구간 내 해당되는 원소들의 구간 합은?
cout << " The answer is " << sum[11][12] - sum[11][4] - sum[3][12] + sum[3][4];
728x90
'Algorithm (C++ based) > Algorithm 이론' 카테고리의 다른 글
| 최소 스패닝 트리 / 최소 신장 트리 (MST) (0) | 2021.08.09 |
|---|---|
| 유니온 파인드 (Union Find, Disjoint set) (0) | 2021.08.06 |
| 위상 정렬 (Topological Sort) (0) | 2021.08.05 |
| 투 포인터 알고리즘 (Two pointer Algorithm) (0) | 2021.07.20 |
| 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2021.02.20 |




댓글